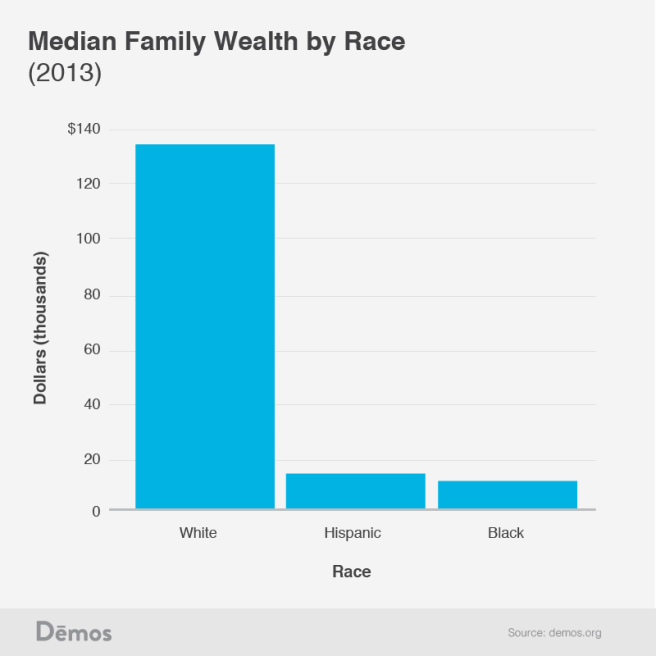
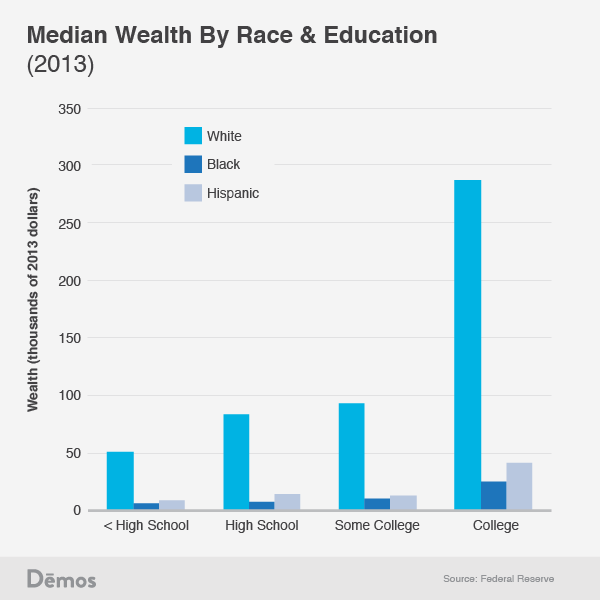
A couple of weeks ago, I came across an article in The Atlantic titled “What on Earth is Wrong with Connecticut.” The article is about the condition of Connecticut’s economy and state budget, and inspired me to consider two questions that I had been thinking about for some time – (1) are any U.S. states currently in recession, and (2) has there been any historical pattern around national recessions regarding which states enter recession earlier than others?
DATA & METHODOLOGY
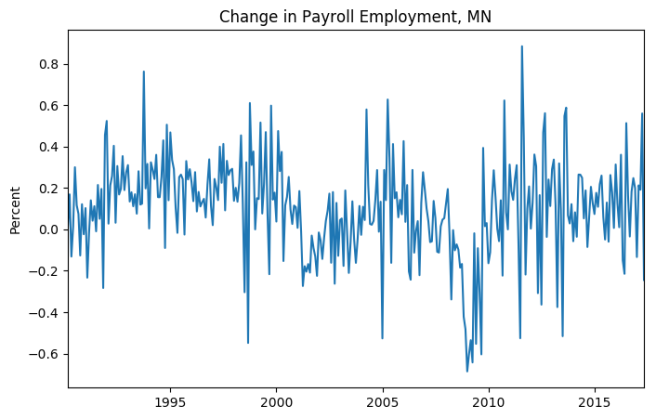
In order to try and answer these questions, I used data on the month-over-month (MoM) percentage change in total payroll employment in all 50 states (and Washington DC) from 1990 through May, 2017. While recessions are typically defined as a decline in output, not employment, national employment recessions and output recessions have historically been highly correlated. Additionally, the data for state employment goes back further then the data for state GDP, at least on FRED, and the the employment data is measured at a higher frequency. To give a sense of what the raw data looks like, below is the MoM percentage change in total payroll employment for Minnesota:
To estimate recession probabilities for each state, I use a version of the Markov Switching (MS) model developed in Hamilton (1989). In this model, there are two regimes, or “states of the world”. When Hamilton estimated this model using data on U.S. GNP, it returned two clear regimes – “expansion” and “recession”. Furthermore, as a byproduct of estimation, the model provided estimated probabilities for each regime at each date in the history of the data, and these probabilities matched up very closely with the official recession dates in the U.S.
I decided to estimate an MS model independently for each U.S. state, using the MoM percentage change in total payroll employment as the data. Similar estimation strategies have been undertaken before, for example, see Owyang, Piger, and Wall (2005) (pdf). After censoring the data to ignore large outliers that greatly influenced estimation in approximately 10 states (such as the massive decline in employment in Louisiana following Hurricane Katrina), I fit the following Markov Switching model to each U.S. state, independently:
And evolves according to an exogenous first order Markov process, with transition matrix given by:
I performed Bayesian estimation, with the following priors on the regression coefficients:
- Annual expansion growth rate
- Annual recession growth rate
- AR(1) term
Note that I am using the annual growth rate here instead of the monthly growth rate, since it is a more intuitive number. These priors imply 99% prior confidence intervals for the unconditional annual growth in expansions and recessions of roughly and
, and a 99% prior confidence interval for the AR(1) of roughly
.
For the transition probabilities, the prior probability of staying in expansion next month if the state was in expansion this month is set to 0.9, and the prior probability of staying in recession next month if the state was in recession this month is set to 0.8, each with 5 prior observations.
RESULTS
In regard to the first question – are any states currently in recession, the answer is probably no. As of May, 2017, only Idaho had a recession probability greater than or equal to 50% (and it was exactly 50%). However, May was the first month in which the recession probability exceeded 49%, and based on earlier research on national recessions, a recession probability typically has to exceed 49% for at least two months in a row to reliably signify the onset of a recession.
| State | Rec. Prob |
| ID | 50% |
| NJ | 40% |
| NH | 39% |
| OK | 34% |
| KS | 32% |
As far as Connecticut is concerned, it currently has a recession probability of 0%, but it is estimated to have the slowest expansion growth rate among all 50 states, which could be a result of the factors discussed in the article, or simply due to out-migration (and disentangling these two causal factors is not something I am able to do).
| State | Exp. Growth Rate |
| NV | 3.9% |
| UT | 3.6% |
| … | … |
| PA | 0.9% |
| CT | 0.8% |
In regard to the second question – has there been any historical pattern regarding which states enter recessions “first” before the beginning of a national recession, I don’t find any sort of pattern. The two images below show monthly employment recession probabilities for all 50 states (plus DC) over time, starting in 1990 (click twice to enlarge).
CONCLUSION
I used an MS model with AR(1) dynamics to estimate historical recession probabilities in all 50 U.S. states. For the most recent month for which data is available, May 2017, I found that there were probably no U.S. states in recession, although if payroll employment growth is again negative in Idaho in June, it would likely indicate an employment recession in Idaho. I also found that there does not seem to be a consistent pattern regarding which states enter recessions first, prior to a national recession. In other words, there are no states that have served as reliable “leading indicators” for the national economy over the last three business cycles. Finally, while Connecticut is the wealthiest state in the U.S. in per-capita terms, it has had the slowest rate of increase in employment during expansions over the past 25 years. The current methodology does not allow me to determine any factors that may be causing this slow growth.
As new data is released, I will keep updated graphs and estimates here: http://adamjcheck.com/state_rec.html